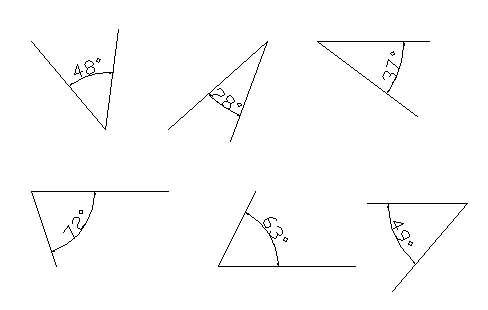Matemáticas II: febrero 2014

Teorema de Pitágoras

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos...

Si el triángulo tiene un ángulo recto (90°)...

... y pones un cuadrado sobre cada uno de sus lados, entonces...

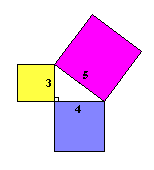
...el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos.

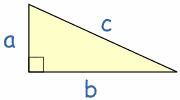
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:

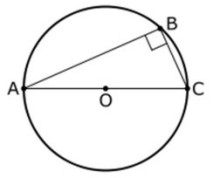
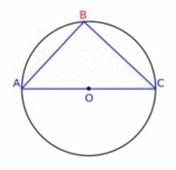
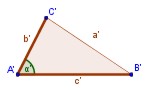
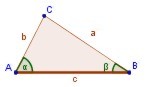
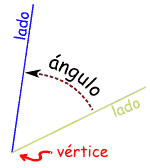
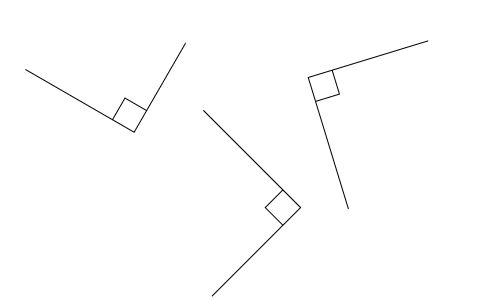
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

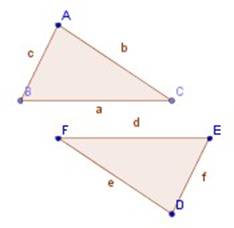
Entonces el teorema dice que... el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a² + b² = c²

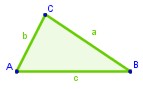
Comprobemos el área... 3² + 4² = 5²

Obtenemos: 9 + 16 = 25

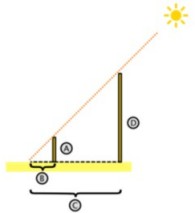
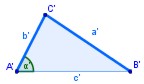
Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (Recordemos que sólo funciona en triángulos rectángulos...)

*Dato curioso*

aunque se llama Teorema de Pitágoras, también lo conocían los matemáticos indios, griegos, chinos y babilonios antes de que él viviera :O

Teorema de triángulos semejantes. Teorema de Thales de Mileto

Triángulos semejantes

Dos triángulos son semejantes si tienen los mismos ángulos.

Si hacemos coincidir los vértices de los dos triángulos que tengan el mismo ángulo, obtenemos lo que se llama posición en Thales de los triángulos semejantes.

Teorema de Thales o Tales de Mileto

Cuando en geometría hablemos del Teorema de Tales (o Thales), debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.
El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente (triángulos semejantes son los que tienen iguales ángulos).
Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa).

Primer teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo:

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.
Lo que se traduce en la fórmula

Corolario

Al establecer la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.

Una aplicación del Teorema de Tales.

Por ejemplo, en la figura de la izquierda se observan dos triángulos que, en virtud del Teorema de Tales, son semejantes. Entonces, como corolario, el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande.
En virtud del teorema de Tales, ambos triángulos son semejantes y se cumple que:

A = D

B C

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto.

Segundo teorema

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:
Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el ángulo ABC, es recto.
Este teorema , es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

Teorema de triángulos congruentes

Éste pequeño símbolo:

quiere decir congruencia, en ésta entrada trabajeremos con eso: congruencia.

Se dice que un Δ ABC es congruente con otro Δ DEF si sus lados respectivos son iguales y sus ángulos respectivos también lo son.
Para expresar en lenguaje matemático que los dos triángulos de la izquierda son congruentes, se usa la siguiente simbología:

Al observar los triángulos de la figura puede apreciarse que tienen lados respectivamente congruentes, que son:

También tienen ángulos respectivamente congruentes:

Entonces es posible afirmar que

.
Al revés: si dos o más triángulos son congruentes, sus lados y ángulos lo serán respectivamente, en el orden de las letras asignadas a sus vértices para nombrarlos, salvo que gráficamente se indique otra correspondencia.
Si, por ejemplo, tenemos Δ ABR Δ CDS, sus lados respectivamente congruentes serán:

Y los ángulos respectivamente congruentes serán:

Criterios de congruencia

Los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes.
Estas son:
1.- Congruencia de sus lados
2.- Congruencia de sus ángulos
Para que dos triángulos sean congruentes, es suficiente que sólo algunos lados y/o ángulos sean iguales.

Los postulados o criterios básicos de congruencia de triángulos son:

Postulado LAL

LAL significa lado-ángulo-lado.
Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.

Postulado ALA

ALA significa ángulo-lado-ángulo.
Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.

triangulos_congruencia_024

Postulado LLA

LLA significa lado-lado-ángulo
Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.

triangulos_congruencia_030

Postulado LLL

LLL significa lado-lado-lado.
Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.

triangulos_congruencia_040

Cálculo de ángulos en distintas formas.

Para el cálculo de ángulos existen diversas formas de hacerlo, por ejemplo:

Sistema sexagesimal:
Teniendo en cuenta esto, el ángulo llano tendría 180 grados o divisiones sexagesimales, se llama así debido a que la base de cálculo en la cual se basa es en una base de 60. Utilizando esta base se puede ahora representar de una manera más precisa la medida de un ángulo. Por ejemplo si nos dicen que un ángulo mide 32°25’15’’ (32grados 25minutos 15 segundos) nos estarían diciendo que el ángulo mide un poco más de 32 grados. El otro sistema más utilizado para medir un ángulo es el sistema de los radianes.

Sistema de Radian:
Un radian se define como el ángulo que subtiende un arco de la circunferencia que tiene como medida el radio de esta. De la anterior definición se llega a la relación de que la longitud de la circunferencia puede expresarse como: L=2πR = 2πrad, entonces 360° serian equivalentes a 2 πrad, esta equivalencia nos sirve para expresar y convertir la medida de un ángulo a cualquiera de los dos sistemas de medida con una simple regla de tres.

Grado centesimal:
Unidad angular que divide la circuferencia en 400 grados centesimales.

Clasificación de triángulos

Como es bien sabido, un triángulo tiene tres lados y tres ángulos. Se obtienen diferentes tipos de triángulos dependiendo del valor de sus ángulos y sus lados.

Se clasifican en...

Triángulo isóceles:
Tiene dos lados iguales y uno desigual.

Triángulo equilatero:
Es aquel que tiene todos sus lados iguales.

Triángulo escaleno:
Tiene tres lados desiguales.

Triángulo obtusángulo:
Tiene un ángulo obtuso.

Triángulo acutángulo:
Es aquel triángulo que tiene tres ángulos agudos.

Triángulo rectángulo:
Es el triángulo que tiene un ángulo de 90°.

Teoremas sobre las rectas paralelas

RECTAS PARALELAS:

Dos líneas son paralelas cuando se mantienen siempre a la misma distancia (también se llaman "equidistantes"), y nunca se encuentran. Recuerda:

Siempre a la misma distancia y nunca se encuentran.

TEOREMA 1
Si dos rectas se cortan por una transversal y un par de angulos correspondientes son congruentes, entonces las rectas son paralelas.
TEOREMA 2
Si dos rectas se cortan por una transversal y un par de angulos alternos interiores son congruentes, entonces las rectas son paralelas.
TEOREMA 3
Si dos rectas se cortan por una transversal y un par de angulos alternos exteriores son congruentes, entonces las rectas son paralelas.
TEOREMA 4
Si dos rectas se cortan por una transversal y un par de angulos interiores en el mismo lado de la transversal son suplementarios, entonces las rectas son paralelas.
TEOREMA 5
Dadas las rectas p, q y r, si p es paralela a q y q es paralela a r, entonces p es paralela a r.

TEOREMA 6
Si dos rectas paralelas se cortan por una transversal, entonces los angulos alternos interiores son congruentes.
TEOREMA 7
Si dos rectas paralelas se cortan por una transversal, entonces los angulos alternos exteriores son congruentes.
TEOREMA 8
Si dos rectas se cortan por una transversal, entonces los angulos correspondientes son congruentes.
TEOREMA 9
Si dos rectas paralelas se cortan por una transversal, entonces los angulos interiores del mismo lado de la transversal son suplementarios.

Clasificación de los tipos de ángulos

Un ángulo es una figura geométrica formada en una superficie por dos líneas que parten de un mismo punto.
También podemos decir que un ángulo es la abertura formada por dos "rayos" llamados lados, que tienen un origen común llamado vértice.

Las partes de un ángulo son las siguientes: